
УДК 517:004
ПРОЦЕССТЕРДІҢ МАТЕМАТИКАЛЫҚ МОДЕЛДЕРІНІҢ ПАРАМЕТРЛЕРІН АНЫҚТАУДА ЖАҢА АҚПАРАТТЫҚ ТЕХНОЛОГИЯЛАРДЫ ҚОЛДАНУ ТӘСІЛДЕРІ НЫҒАЙТУ
Тагаев Нұрлыбек Сайдуллаевич, т.ғ.к., М.Әуезов атындағы Оңтүстік Қазақстан университетінің доценті, nureke.55@mail.ru
Чалабаева Аурика Исаевна, магистр транспорта, Шымкенский колледж транспорта, aurika.85@mail.ru
Түйіні. Болашақ инженерлер, экономистер, көлік саласының т.б. маман иелері қызмет бабында әр түрлі күрделі есептерді шығаруларына тура келеді. Солардың ішінде ең көп кездесетін есептің түрі сызықтық теңдеулер жүйесін шешу болып табылады, себебі физикалық, химиялық, техникалық немесе экономикалық мәселелердің математикалық моделін құрғанда, процестерді сипаттайтын функциялардың қарапайым болуы үшін, оның сызықты түрін алуға тырысады. Бұл, бір жағынан, қойылған мәселені шешудің оңай жолына әкелсе, екінші жағынан, бұндай есептерді шығарудың көптеген әдістері бар. Алайда, алынған сызықты теңдеулер жүйесінде белгісіздер саны көбейген сайын, жүйені шешуде қыруар есептеулер атқарылуы қажет болады, яғни қосымша уақыт пен қаржыны талап етеді. Сондықтан осындай проблемаларды кешенді түрде шешуде жаңа информациялық технологияларды пайдалану өте тиімді. Осы мақалада, электрондық кестені пайдалану әдістемесі нақты мысалды есептеу арқылы көрсетілді.
Кілттік сөздер. Сызықтық теңдеулер жүйесі, математикалық модель, кешенді түрде шешуде, жаңа информациялық технологиялар, белгісіздер мен теңдеулер саны, электрондық кестені пайдалану.
Аннотация. Будущим инженерам, экономистам, специалистам транспортной отрасли и т.д. приходится решать различные сложные задачи по службе. Среди них наиболее распространенным видом задачи является решение системы линейных уравнений, поскольку при построении математической модели физических, химических, технических или экономических задач, для простоты функций, описывающих процессы, пытаются получить ее линейный тип. Это, с одной стороны, ведет к легкому пути решения поставленной задачи, с другой-существует множество способов решения таких задач. Однако, по мере увеличения числа неизвестных в полученной линейной системе уравнений, при решении системы необходимо будет выполнять более тщательные расчеты, т. е. требовать дополнительных затрат времени и средств. Поэтому использование новых информационных технологий в комплексном решении таких проблем очень эффективно. В данной статье показана методика использования электронной таблицы при решении систем линейных уравнений с расчетом на конкретном примере.
Ключевые слова. Система линейных уравнений, математическая модель, в комплексном решении, новые информационные технологии, число неизвестных и уравнений, использование электронных таблиц.
Abstract. Future engineers, economists, specialists in the transport industry, etc. have to solve various complex tasks in the service. Among them, the most common type of problem is the solution of a system of linear equations, since when constructing a mathematical model of physical, chemical, technical or economic problems, for the simplicity of functions describing processes, they try to obtain its linear type. This, on the one hand, leads to an easy way to solve the problem, on the other-there are many ways to solve such problems. However, as the number of unknowns in the resulting linear system of equations increases, it will be necessary to perform more careful calculations when solving the system, i.e. to require additional time and money.Therefore, the use of new information technologies in the complex solution of such problems is very effective. This article shows the method of using the MS Excel spreadsheet for solving systems of linear equations with a calculation based on a specific example.
Keywords. A system of linear equations, a mathematical model, in a complex solution, new information technologies, the number of unknowns and equations, the use of spreadsheets
Кіріспе. Болашақ инженерлер, экономистер, көлік саласының т.б. маман иелері қызмет бабында әр түрлі күрделі есептерді шығаруларына тура келеді.
Солардың ішінде ең көп кездесетін есептің түрі сызықтық теңдеулер жүйесін шешу болып табылады, себебі физикалық, химиялық, техникалық немесе экономикалық мәселелердің математикалық моделін құрғанда, процестерді сипаттайтын функциялардың қарапайым болуы үшін, оның сызықты түрін алуға тырысады.
Бұл, бір жағынан, қойылған мәселені шешудің оңай жолына әкелсе, екінші жағынан, бұндай есептерді шығарудың көптеген әдістері бар. Алайда, алынған сызықты теңдеулер жүйесінде белгісіздер саны көбейген сайын, жүйені шешуде қыруар есептеулер атқарылуы қажет болады, яғни қосымша уақыт пен қаржыны талап етеді [1].
Сондықтан осындай проблемаларды кешенді түрде шешуде жаңа информациялық технологияларды пайдалану өте тиімді. Осы мақалада, сызықтық теңдеулер жүйесін шешуде (белгісіздермен теңдеулер саны бір-біріне тең болған жағдай) MS Excel электрондық кестесін пайдалану әдістемесі нақты мысалды есептеу арқылы көрсетілді.
Әдістер. Сызықтық теңдеулер жүйесінің матрицалық түрі келесі түрде жазылады:
АХ=B, (1)
мұндағы А=(aij), (i= ;j=
;j= ); (2)
); (2)
X=(xj), (j= ) (3)
) (3)
B=(вi), (i= ) (4)
) (4)
Берілген жүйе матрицасының анықтаушы А0 болған кезде, (1) матрицалық теңдеуді шешу үшін оның екі жағында «сол жағынан» А-матрицаға кері А-1 матрицасына көбейтеміз:
А-1АХ=А-1В
Берілген А матрицасымен оның кері А-1 матрицасының көбейтіндісі бірлік матрицаны береді, ал бірлік матрицаны кез келген векторға көбейтсек, вектордың өзіне тең, олай болса соңғы теңдіктен табатынымыз:
Х= А-1 В (5)
Жалпы, берілген матрицаға кері матрица келесі теңдікпен анықталады:
 , (j=
, (j= ;
i=
;
i= ), (6)
), (6)
мұндағы (Аji ) - берілген матрицаның аij элементтерінің алгебралық
Аij толықтауыштарынан құралған матрицаны транспонирлеу арқылы алынған қосалқы деп аталатын матрица, А - берілген матрицаның анықтауышы.
Сонымен сызықтық теңдеулер жүйесін матрицалық әдіспен шешу үшін, алдымен берілген жүйе матрицасының анықтауышы нөлге тең еместігіне көз жеткізу керек. Содан соң, жүйе матрицасының кері матрицасын (6) формулаға сәйкес тауып, оны (1)-ші теңдеуге сол жағынан көбейтіп, (5)-түрдегі теңдеуді алу керек. Соңғы теңдеуден, екі матрицаның бір-біріне тең болу шартына сәйкес, ізделініп отырған жүйенің (х1,х2,...,хn) шешімдерін табамыз.
Зерттеу нәтижелері.
Сызықтық теңдеулер жүйесін MS Excel электронды кестесін қолданып шешуді үйрену үшін үш белгісі бар теңдеулер жүйесін қарастырайық [2]:
 (7)
(7)
(7) жүйенің анықтауышы:
 , (8)
, (8)
демек жүйенің шешімі бар.
Берілген жүенің
матрицасы  (9)
(9)
(9)-дың кері матрицасын табу үшін алдымен оның
аij элементтерінің алгебралық
толықтауыштарын есептеп алуымыз қажет:


 ,
,
осындай жолмен қалған толықтауыштарды анықтаймыз:
А21=-10, А22=-5, А23=-5, А31=1, А32=-7, А33=3.
Енді осы Аіj алгебралық толықтауыштарынан тұратын матрицаны құрайық
 (10)
(10)
Аіj - матрицасын транспонирлеп, яғни оның сәйкес жолдары мен бағандарының орындарын ауыстырып А матрицасының қосалқы матрицасын аламыз:

![]()
(11)
Ал енді (8) және (11) табылғандарын (6) - ға қойсақ:
 (12)
(12)
(7) - жүйенің бос мүшелерінен құралған тік матрица
 (13)
(13)
Белгісіздерден құралған тік матрица
 (14)
(14)
Берілген сызықты теңдеулер жүйесінің шешімі - матрицалық әдіспен жазғанда (5)- сәйкес төмендегі теңдеумен анықталады:

Соңғы теңдіктен табатынымыз х1= -1; х2= -2; х3= 1.
Е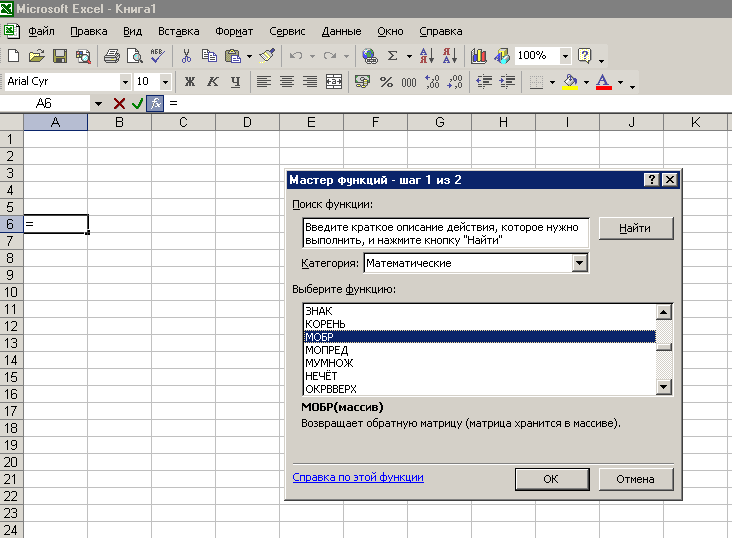 нді осы
есепті MS Excel электронды кестесінің парағында шешелік [3].
Ол үшін
төмендегі
Excel
терезесінде - парағында (1-сурет) келесі амалдарды орындайық:
нді осы
есепті MS Excel электронды кестесінің парағында шешелік [3].
Ол үшін
төмендегі
Excel
терезесінде - парағында (1-сурет) келесі амалдарды орындайық:
1-сурет. MS Excel электронды кестесінің парағы
-
Жаңа парақ ашып, оны ''1-сурет'' деп белгілейік.
-
А1 ұяшығына «Теңдеулер жүйесін матрицалық ідіспен шешу» деп жазамыз.
-
А3 ұяшығына АХ=В деп жазамыз.
-
«Берілген жүйенің матрицасы А» деп жазамыз.
-
А6:С8 ұяшықтарына (7) матрица элементерін жазамыз:
-
А6 -ға 2 В6 -ға -1 С6 -ға -3
-
А7 -ге 1 В7 - ге 1 С7- ге 2
-
А8 - ге 1 В8 - ге 2 С8 - ге-4
-
Е5-тен ''В - матрицасы » деп жазамыз.
-
Е6 – Е8 ұяшықтарына осы вектордың компоненттерін жазамыз:
-
Е6 - ға 3
-
Е7-ге 1
-
Е8-ге 9
MS Excel электронды кестесінің контур сызықтарын өшіріп, берілген шамаларды сызықпен қоршап қоямыз.
Осылардан соң MS Excel шешімдер кестесінде біраз амалдар орындалып, өте жылдам 2 суреттегі түрдегі шешімдер кестесін аламыз.
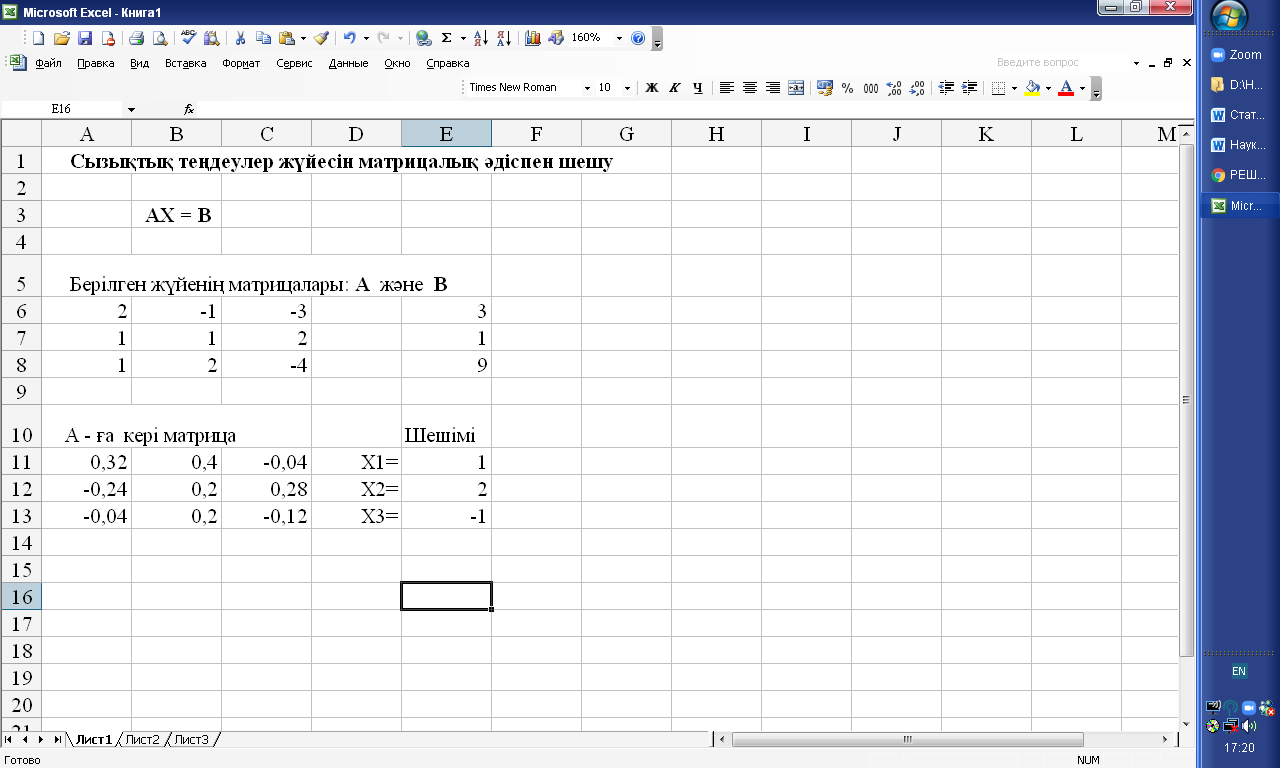
2-сурет. MS Excel шешімдер кестесі
Осы кестеден көрініп тұрғандай берілген жүйенің шешімдері х1=1, х2= 2, х3= -1.
Қорытынды. Жоғарыдағы жүйені электронды кестені пайдаланып шешу үшін уақыт тек қана ол жүйенің матрица элементтерін кесте парағына теру үшін кетті. Ал қалған амалдар өте жылдам аз уақыт ішінде орындалады. MS Excel электронды кестесінде өлшем бірлігі 60-қа дейінгі матрицалармен амалдар атқаруға болады. Демек, өндіріс орындарында, ғылыми жұмыстарды орындау барысында жаңа информациялық технологияларды, атап айтсақ MS Excel электронды кестесін кеңінен пайдалансақ, жоғарыдағыдай есептердің белгісіздері мен теңдеулер саны өте көп болған жағдайда, оны шешуге қажет қыруар уақыт пен қаржыны үнемдеуге болады.
ӘДЕБИЕТТЕР
[1] Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 3-изд. М, Наука, 2008, 216с.
[2] Балафанов Е.К., Бурибаев Б., Даулеткулов А.30 уроков по информатике, Алматы, ДЖ., 1999г, 442с (на русском и казахском языках).
[3] Носитер Дж. Excel 7.0 для Windows-95. M., Бином, 1996, 390с.
LITERATURE
[1] Bugrov Ja.S., Nikol'skij S.M. Jelementy linejnoj algebry i analiticheskoj geometrii. 3-izd. M, Nauka, 2008, 216s.
[2] Balafanov E.K., Buribaev B., Dauletkulov A.30 urokov po informatike, Almaty, DZh., 1999g, 442s (na russkom i kazahskom jazykah).
[3] Nositer Dzh. Excel 7.0 dlja Windows-95. M., Binom, 1996, 390s.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
ПРОЦЕССТЕРДІҢ МАТЕМАТИКАЛЫҚ МОДЕЛДЕРІНІҢ ПАРАМЕТРЛЕРІН АНЫҚТАУДА ЖАҢА АҚПАРАТТЫҚ ТЕХНОЛОГИЯЛАРДЫ ҚОЛДАНУ ТӘСІЛДЕРІ НЫҒАЙТУ
ПРОЦЕССТЕРДІҢ МАТЕМАТИКАЛЫҚ МОДЕЛДЕРІНІҢ ПАРАМЕТРЛЕРІН АНЫҚТАУДА ЖАҢА АҚПАРАТТЫҚ ТЕХНОЛОГИЯЛАРДЫ ҚОЛДАНУ ТӘСІЛДЕРІ НЫҒАЙТУ
УДК 517:004
ПРОЦЕССТЕРДІҢ МАТЕМАТИКАЛЫҚ МОДЕЛДЕРІНІҢ ПАРАМЕТРЛЕРІН АНЫҚТАУДА ЖАҢА АҚПАРАТТЫҚ ТЕХНОЛОГИЯЛАРДЫ ҚОЛДАНУ ТӘСІЛДЕРІ НЫҒАЙТУ
Тагаев Нұрлыбек Сайдуллаевич, т.ғ.к., М.Әуезов атындағы Оңтүстік Қазақстан университетінің доценті, nureke.55@mail.ru
Чалабаева Аурика Исаевна, магистр транспорта, Шымкенский колледж транспорта, aurika.85@mail.ru
Түйіні. Болашақ инженерлер, экономистер, көлік саласының т.б. маман иелері қызмет бабында әр түрлі күрделі есептерді шығаруларына тура келеді. Солардың ішінде ең көп кездесетін есептің түрі сызықтық теңдеулер жүйесін шешу болып табылады, себебі физикалық, химиялық, техникалық немесе экономикалық мәселелердің математикалық моделін құрғанда, процестерді сипаттайтын функциялардың қарапайым болуы үшін, оның сызықты түрін алуға тырысады. Бұл, бір жағынан, қойылған мәселені шешудің оңай жолына әкелсе, екінші жағынан, бұндай есептерді шығарудың көптеген әдістері бар. Алайда, алынған сызықты теңдеулер жүйесінде белгісіздер саны көбейген сайын, жүйені шешуде қыруар есептеулер атқарылуы қажет болады, яғни қосымша уақыт пен қаржыны талап етеді. Сондықтан осындай проблемаларды кешенді түрде шешуде жаңа информациялық технологияларды пайдалану өте тиімді. Осы мақалада, электрондық кестені пайдалану әдістемесі нақты мысалды есептеу арқылы көрсетілді.
Кілттік сөздер. Сызықтық теңдеулер жүйесі, математикалық модель, кешенді түрде шешуде, жаңа информациялық технологиялар, белгісіздер мен теңдеулер саны, электрондық кестені пайдалану.
Аннотация. Будущим инженерам, экономистам, специалистам транспортной отрасли и т.д. приходится решать различные сложные задачи по службе. Среди них наиболее распространенным видом задачи является решение системы линейных уравнений, поскольку при построении математической модели физических, химических, технических или экономических задач, для простоты функций, описывающих процессы, пытаются получить ее линейный тип. Это, с одной стороны, ведет к легкому пути решения поставленной задачи, с другой-существует множество способов решения таких задач. Однако, по мере увеличения числа неизвестных в полученной линейной системе уравнений, при решении системы необходимо будет выполнять более тщательные расчеты, т. е. требовать дополнительных затрат времени и средств. Поэтому использование новых информационных технологий в комплексном решении таких проблем очень эффективно. В данной статье показана методика использования электронной таблицы при решении систем линейных уравнений с расчетом на конкретном примере.
Ключевые слова. Система линейных уравнений, математическая модель, в комплексном решении, новые информационные технологии, число неизвестных и уравнений, использование электронных таблиц.
Abstract. Future engineers, economists, specialists in the transport industry, etc. have to solve various complex tasks in the service. Among them, the most common type of problem is the solution of a system of linear equations, since when constructing a mathematical model of physical, chemical, technical or economic problems, for the simplicity of functions describing processes, they try to obtain its linear type. This, on the one hand, leads to an easy way to solve the problem, on the other-there are many ways to solve such problems. However, as the number of unknowns in the resulting linear system of equations increases, it will be necessary to perform more careful calculations when solving the system, i.e. to require additional time and money.Therefore, the use of new information technologies in the complex solution of such problems is very effective. This article shows the method of using the MS Excel spreadsheet for solving systems of linear equations with a calculation based on a specific example.
Keywords. A system of linear equations, a mathematical model, in a complex solution, new information technologies, the number of unknowns and equations, the use of spreadsheets
Кіріспе. Болашақ инженерлер, экономистер, көлік саласының т.б. маман иелері қызмет бабында әр түрлі күрделі есептерді шығаруларына тура келеді.
Солардың ішінде ең көп кездесетін есептің түрі сызықтық теңдеулер жүйесін шешу болып табылады, себебі физикалық, химиялық, техникалық немесе экономикалық мәселелердің математикалық моделін құрғанда, процестерді сипаттайтын функциялардың қарапайым болуы үшін, оның сызықты түрін алуға тырысады.
Бұл, бір жағынан, қойылған мәселені шешудің оңай жолына әкелсе, екінші жағынан, бұндай есептерді шығарудың көптеген әдістері бар. Алайда, алынған сызықты теңдеулер жүйесінде белгісіздер саны көбейген сайын, жүйені шешуде қыруар есептеулер атқарылуы қажет болады, яғни қосымша уақыт пен қаржыны талап етеді [1].
Сондықтан осындай проблемаларды кешенді түрде шешуде жаңа информациялық технологияларды пайдалану өте тиімді. Осы мақалада, сызықтық теңдеулер жүйесін шешуде (белгісіздермен теңдеулер саны бір-біріне тең болған жағдай) MS Excel электрондық кестесін пайдалану әдістемесі нақты мысалды есептеу арқылы көрсетілді.
Әдістер. Сызықтық теңдеулер жүйесінің матрицалық түрі келесі түрде жазылады:
АХ=B, (1)
мұндағы А=(aij), (i= ;j=
;j= ); (2)
); (2)
X=(xj), (j= ) (3)
) (3)
B=(вi), (i= ) (4)
) (4)
Берілген жүйе матрицасының анықтаушы А0 болған кезде, (1) матрицалық теңдеуді шешу үшін оның екі жағында «сол жағынан» А-матрицаға кері А-1 матрицасына көбейтеміз:
А-1АХ=А-1В
Берілген А матрицасымен оның кері А-1 матрицасының көбейтіндісі бірлік матрицаны береді, ал бірлік матрицаны кез келген векторға көбейтсек, вектордың өзіне тең, олай болса соңғы теңдіктен табатынымыз:
Х= А-1 В (5)
Жалпы, берілген матрицаға кері матрица келесі теңдікпен анықталады:
 , (j=
, (j= ;
i=
;
i= ), (6)
), (6)
мұндағы (Аji ) - берілген матрицаның аij элементтерінің алгебралық
Аij толықтауыштарынан құралған матрицаны транспонирлеу арқылы алынған қосалқы деп аталатын матрица, А - берілген матрицаның анықтауышы.
Сонымен сызықтық теңдеулер жүйесін матрицалық әдіспен шешу үшін, алдымен берілген жүйе матрицасының анықтауышы нөлге тең еместігіне көз жеткізу керек. Содан соң, жүйе матрицасының кері матрицасын (6) формулаға сәйкес тауып, оны (1)-ші теңдеуге сол жағынан көбейтіп, (5)-түрдегі теңдеуді алу керек. Соңғы теңдеуден, екі матрицаның бір-біріне тең болу шартына сәйкес, ізделініп отырған жүйенің (х1,х2,...,хn) шешімдерін табамыз.
Зерттеу нәтижелері.
Сызықтық теңдеулер жүйесін MS Excel электронды кестесін қолданып шешуді үйрену үшін үш белгісі бар теңдеулер жүйесін қарастырайық [2]:
 (7)
(7)
(7) жүйенің анықтауышы:
 , (8)
, (8)
демек жүйенің шешімі бар.
Берілген жүенің
матрицасы  (9)
(9)
(9)-дың кері матрицасын табу үшін алдымен оның
аij элементтерінің алгебралық
толықтауыштарын есептеп алуымыз қажет:


 ,
,
осындай жолмен қалған толықтауыштарды анықтаймыз:
А21=-10, А22=-5, А23=-5, А31=1, А32=-7, А33=3.
Енді осы Аіj алгебралық толықтауыштарынан тұратын матрицаны құрайық
 (10)
(10)
Аіj - матрицасын транспонирлеп, яғни оның сәйкес жолдары мен бағандарының орындарын ауыстырып А матрицасының қосалқы матрицасын аламыз:

![]()
(11)
Ал енді (8) және (11) табылғандарын (6) - ға қойсақ:
 (12)
(12)
(7) - жүйенің бос мүшелерінен құралған тік матрица
 (13)
(13)
Белгісіздерден құралған тік матрица
 (14)
(14)
Берілген сызықты теңдеулер жүйесінің шешімі - матрицалық әдіспен жазғанда (5)- сәйкес төмендегі теңдеумен анықталады:

Соңғы теңдіктен табатынымыз х1= -1; х2= -2; х3= 1.
Е нді осы
есепті MS Excel электронды кестесінің парағында шешелік [3].
Ол үшін
төмендегі
Excel
терезесінде - парағында (1-сурет) келесі амалдарды орындайық:
нді осы
есепті MS Excel электронды кестесінің парағында шешелік [3].
Ол үшін
төмендегі
Excel
терезесінде - парағында (1-сурет) келесі амалдарды орындайық:
1-сурет. MS Excel электронды кестесінің парағы
-
Жаңа парақ ашып, оны ''1-сурет'' деп белгілейік.
-
А1 ұяшығына «Теңдеулер жүйесін матрицалық ідіспен шешу» деп жазамыз.
-
А3 ұяшығына АХ=В деп жазамыз.
-
«Берілген жүйенің матрицасы А» деп жазамыз.
-
А6:С8 ұяшықтарына (7) матрица элементерін жазамыз:
-
А6 -ға 2 В6 -ға -1 С6 -ға -3
-
А7 -ге 1 В7 - ге 1 С7- ге 2
-
А8 - ге 1 В8 - ге 2 С8 - ге-4
-
Е5-тен ''В - матрицасы » деп жазамыз.
-
Е6 – Е8 ұяшықтарына осы вектордың компоненттерін жазамыз:
-
Е6 - ға 3
-
Е7-ге 1
-
Е8-ге 9
MS Excel электронды кестесінің контур сызықтарын өшіріп, берілген шамаларды сызықпен қоршап қоямыз.
Осылардан соң MS Excel шешімдер кестесінде біраз амалдар орындалып, өте жылдам 2 суреттегі түрдегі шешімдер кестесін аламыз.

2-сурет. MS Excel шешімдер кестесі
Осы кестеден көрініп тұрғандай берілген жүйенің шешімдері х1=1, х2= 2, х3= -1.
Қорытынды. Жоғарыдағы жүйені электронды кестені пайдаланып шешу үшін уақыт тек қана ол жүйенің матрица элементтерін кесте парағына теру үшін кетті. Ал қалған амалдар өте жылдам аз уақыт ішінде орындалады. MS Excel электронды кестесінде өлшем бірлігі 60-қа дейінгі матрицалармен амалдар атқаруға болады. Демек, өндіріс орындарында, ғылыми жұмыстарды орындау барысында жаңа информациялық технологияларды, атап айтсақ MS Excel электронды кестесін кеңінен пайдалансақ, жоғарыдағыдай есептердің белгісіздері мен теңдеулер саны өте көп болған жағдайда, оны шешуге қажет қыруар уақыт пен қаржыны үнемдеуге болады.
ӘДЕБИЕТТЕР
[1] Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 3-изд. М, Наука, 2008, 216с.
[2] Балафанов Е.К., Бурибаев Б., Даулеткулов А.30 уроков по информатике, Алматы, ДЖ., 1999г, 442с (на русском и казахском языках).
[3] Носитер Дж. Excel 7.0 для Windows-95. M., Бином, 1996, 390с.
LITERATURE
[1] Bugrov Ja.S., Nikol'skij S.M. Jelementy linejnoj algebry i analiticheskoj geometrii. 3-izd. M, Nauka, 2008, 216s.
[2] Balafanov E.K., Buribaev B., Dauletkulov A.30 urokov po informatike, Almaty, DZh., 1999g, 442s (na russkom i kazahskom jazykah).
[3] Nositer Dzh. Excel 7.0 dlja Windows-95. M., Binom, 1996, 390s.

шағым қалдыра аласыз















