ПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ
Цель: закрепить изученный материал о прямоугольнике, ромбе, квадрате в процессе решения задач.
Ход урока
I. Проверка домашнего задания.
Математический диктант
1. I. Является ли прямоугольником параллелограмм, у которого есть прямой угол?
II. Обязательно ли является прямоугольником четырехугольник, у которого есть прямой угол?
2. I. Верно ли, что каждый прямоугольник является параллелограммом?
II. Верно ли, что каждый параллелограмм является прямоугольником?
3. I. Диагонали прямоугольника АЕKМ пересекаются в точке О. Отрезок АО = 3. Найдите длину диагонали ЕМ.
II. Диагонали параллелограмма равны 3 и 5 дм. Является ли этот параллелограмм прямоугольником?
4. I. Диагонали четырехугольника равны. Обязательно ли этот четырехугольник является прямоугольником?
II. Сумма длин диагоналей прямоугольника 13 см. Найдите длину каждой диагонали.
5. I. Периметр ромба равен 12 см. Найдите длины его сторон.
II. Верно ли, что каждый ромб является параллелограммом?
6. I. Верно ли, что каждый параллелограмм является ромбом?
II. Периметр ромба равен 30 см. Найдите его стороны.
7. I. Диагонали ромба делят его на четыре треугольника. Найдите углы каждого треугольника, если один из углов ромба 30°.
II. Ромб АВСD имеет прямой угол. Является ли этот ромб квадратом?
8. I. Две соседние стороны параллелограмма равны и образуют прямой угол. Как называется такой параллелограмм?
II. Диагонали квадрата делят его на четыре треугольника. Найдите углы каждого треугольника.
II. Решение задач. №№ 404, 407 (устно).
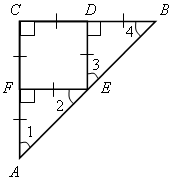
№ 412.
|
|
1. 2.
3.
4. СDЕF –
квадрат |
5. АC = 12 cм. AF = CF = 6 cм.
№ 414 (а) наметить план решения.
III. Самостоятельная работа обучающего характера с проверкой в классе.
Вариант I
1. Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 30° меньше другого.
2. № 413 (б).
Вариант II
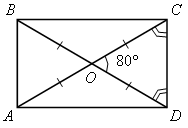
1. Угол между диагоналями прямоугольника равен 80°. Найдите углы между диагональю прямоугольника и его сторонами.
2. № 414 (б).
Вариант III
(для более подготовленных учащихся)
1. В ромбе
АВСD
биссектриса угла
ВАС
пересекает сторону
ВС и диагональ ВD соответственно в точках M и N. Найдите ![]() АNВ, если
АNВ, если ![]() АМС = 120°.
АМС = 120°.
2. Постройте прямоугольник АВСD по стороне АВ и углу АОВ, где О – точка пересечения диагоналей.
Решение на закрытой доске:
Вариант I
|
|
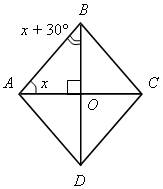
1.
х + х + 30 = 90°; х = 30°. |
2. Дано:
![]()
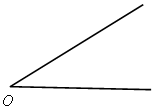
Построить прямоугольник АВСD.
Решение
1) Разделить АС пополам, отметить середину – точку О.
2) От луча ОС отложить угол, равный углу О.
3) На его другой стороне отложить отрезок ОD = АО.
4) На дополнительном луче к лучу ОD отложить отрезок ОВ = ОD.
5) АВСD – прямоугольник (его диагонали равны и точкой пересечения делятся пополам).
Вариант II
|
|
1. ОС = ОВ |
2. Дано:
![]()
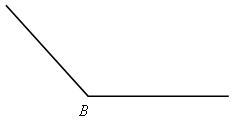
Построить: ромб АВСD.
Решение
1) Отложим угол, равный углу В.
2) На сторонах угла отложим отрезки, равные MN, получим точки А и С.
3) Через точки А и С проведем прямые, параллельные прямым АВ и ВС, получим точку D.
4) АВСD – ромб. (Если у параллелограмма смежные стороны равны, то он является ромбом.)
Вариант III
|
|
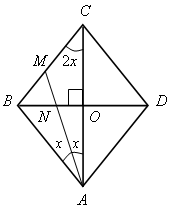
1.
Пусть
х = 20°.
|
2. Дано:
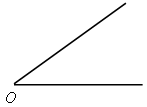
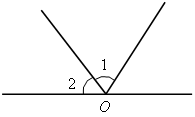
Построить: АВСD – прямоугольник.
Решение
1) Построим угол, смежный с углом О и его биссектрису, получаем углы 1 и 2.
2) Откладываем
АВ и строим в одну полуплоскость от
лучей АВ и ВА углы, равные ![]() 1 и
1 и ![]() 2.
2.
3) Получили ![]() АВО.
АВО.
4) На дополнительных лучах лучам ОВ и ОА откладываем отрезки ОС = АО и ОD = ОВ.
5) АВСD – прямоугольник. (Диагонали его точкой пересечения делятся пополам и равны.)
IV. Итоги урока.
Домашнее задание: вопросы 14–15, с. 115; №№ 406, 411, 413 (а), 415 (б).
По желанию.
|
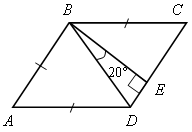
АВСD – ромб. Найти: Решение 1)
2) |
|
![]() АВD =
АВD = ![]() АDВ.
АDВ.
3) ![]() ВDЕ =
ВDЕ = ![]() АВD = 70° как внутренние накрест лежащие при
АВD = 70° как внутренние накрест лежащие при
АВ || СD и секущей ВD.
4) ![]() АВD =
АВD = ![]() АDВ = 70°.
АDВ = 70°.
5) ![]() ВАD = 180° – 70° – 70° = 40°.
ВАD = 180° – 70° – 70° = 40°.
Готовиться к проверочной работе по теме § 1–3 главы V.
жүктеу мүмкіндігіне ие боласыз
Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз
ПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ
ПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ
ПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ
Цель: закрепить изученный материал о прямоугольнике, ромбе, квадрате в процессе решения задач.
Ход урока
I. Проверка домашнего задания.
Математический диктант
1. I. Является ли прямоугольником параллелограмм, у которого есть прямой угол?
II. Обязательно ли является прямоугольником четырехугольник, у которого есть прямой угол?
2. I. Верно ли, что каждый прямоугольник является параллелограммом?
II. Верно ли, что каждый параллелограмм является прямоугольником?
3. I. Диагонали прямоугольника АЕKМ пересекаются в точке О. Отрезок АО = 3. Найдите длину диагонали ЕМ.
II. Диагонали параллелограмма равны 3 и 5 дм. Является ли этот параллелограмм прямоугольником?
4. I. Диагонали четырехугольника равны. Обязательно ли этот четырехугольник является прямоугольником?
II. Сумма длин диагоналей прямоугольника 13 см. Найдите длину каждой диагонали.
5. I. Периметр ромба равен 12 см. Найдите длины его сторон.
II. Верно ли, что каждый ромб является параллелограммом?
6. I. Верно ли, что каждый параллелограмм является ромбом?
II. Периметр ромба равен 30 см. Найдите его стороны.
7. I. Диагонали ромба делят его на четыре треугольника. Найдите углы каждого треугольника, если один из углов ромба 30°.
II. Ромб АВСD имеет прямой угол. Является ли этот ромб квадратом?
8. I. Две соседние стороны параллелограмма равны и образуют прямой угол. Как называется такой параллелограмм?
II. Диагонали квадрата делят его на четыре треугольника. Найдите углы каждого треугольника.
II. Решение задач. №№ 404, 407 (устно).
№ 412.
|
|
1. 2.
3.
4. СDЕF –
квадрат |
5. АC = 12 cм. AF = CF = 6 cм.
№ 414 (а) наметить план решения.
III. Самостоятельная работа обучающего характера с проверкой в классе.
Вариант I
1. Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 30° меньше другого.
2. № 413 (б).
Вариант II
1. Угол между диагоналями прямоугольника равен 80°. Найдите углы между диагональю прямоугольника и его сторонами.
2. № 414 (б).
Вариант III
(для более подготовленных учащихся)
1. В ромбе
АВСD
биссектриса угла
ВАС
пересекает сторону
ВС и диагональ ВD соответственно в точках M и N. Найдите ![]() АNВ, если
АNВ, если ![]() АМС = 120°.
АМС = 120°.
2. Постройте прямоугольник АВСD по стороне АВ и углу АОВ, где О – точка пересечения диагоналей.
Решение на закрытой доске:
Вариант I
|
|
1.
х + х + 30 = 90°; х = 30°. |
2. Дано:
![]()

Построить прямоугольник АВСD.
Решение
1) Разделить АС пополам, отметить середину – точку О.
2) От луча ОС отложить угол, равный углу О.
3) На его другой стороне отложить отрезок ОD = АО.
4) На дополнительном луче к лучу ОD отложить отрезок ОВ = ОD.
5) АВСD – прямоугольник (его диагонали равны и точкой пересечения делятся пополам).
Вариант II
|
|
1. ОС = ОВ |
2. Дано:
![]()

Построить: ромб АВСD.
Решение
1) Отложим угол, равный углу В.
2) На сторонах угла отложим отрезки, равные MN, получим точки А и С.
3) Через точки А и С проведем прямые, параллельные прямым АВ и ВС, получим точку D.
4) АВСD – ромб. (Если у параллелограмма смежные стороны равны, то он является ромбом.)
Вариант III
|
|
1.
Пусть
х = 20°.
|
2. Дано:


Построить: АВСD – прямоугольник.
Решение
1) Построим угол, смежный с углом О и его биссектрису, получаем углы 1 и 2.
2) Откладываем
АВ и строим в одну полуплоскость от
лучей АВ и ВА углы, равные ![]() 1 и
1 и ![]() 2.
2.
3) Получили ![]() АВО.
АВО.
4) На дополнительных лучах лучам ОВ и ОА откладываем отрезки ОС = АО и ОD = ОВ.
5) АВСD – прямоугольник. (Диагонали его точкой пересечения делятся пополам и равны.)
IV. Итоги урока.
Домашнее задание: вопросы 14–15, с. 115; №№ 406, 411, 413 (а), 415 (б).
По желанию.
|
АВСD – ромб. Найти: Решение 1)
2) |
|
![]() АВD =
АВD = ![]() АDВ.
АDВ.
3) ![]() ВDЕ =
ВDЕ = ![]() АВD = 70° как внутренние накрест лежащие при
АВD = 70° как внутренние накрест лежащие при
АВ || СD и секущей ВD.
4) ![]() АВD =
АВD = ![]() АDВ = 70°.
АDВ = 70°.
5) ![]() ВАD = 180° – 70° – 70° = 40°.
ВАD = 180° – 70° – 70° = 40°.
Готовиться к проверочной работе по теме § 1–3 главы V.

шағым қалдыра аласыз