Бұл материал сайт қолданушысы жариялаған. Материалдың ішінде жазылған барлық ақпаратқа жауапкершілікті жариялаған қолданушы жауап береді. Ұстаз тілегі тек ақпаратты таратуға қолдау көрсетеді. Егер материал сіздің авторлық құқығыңызды бұзған болса немесе басқа да себептермен сайттан өшіру керек деп ойласаңыз осында жазыңыз

Бонусты жинап картаңызға (kaspi Gold, Halyk bank) шығарып аласыз
«Логарифмдер және логарифмдік теңдеулер» әдістемелік құрал

«Алматы облысы білім басқармасының Еңбекшіқазақ ауданы бойынша білім бөлімі» мемлекеттік мекемесінің «Ш.Уәлиханов атындағы №1 орта мектеп» коммуналдық мемлекеттік мекемесі
«Логарифмдер және логарифмдік теңдеулер»
әдістемелік құрал
(әдістемелік құрал математика пәні мұғалімдеріне арналған)
Құрастырушы: Ағзанова Алуа Сымбатқызы
2024-2025 оқу жылы
Бұл әдістемелік құрал орта мектеп оқушыларына логарифмдер мен логарифмдік теңдеулер тақырыбын терең меңгеруге көмектесуге арналған. Оқу материалының мазмұны логарифмнің анықтамасынан бастап, оның қасиеттерін, қолдану жолдарын және логарифмдік теңдеулерді шешу әдістерін қамтиды.
Әдістемелік құралда теориялық түсіндірмелер, мысалдар, есептерді шешудің әртүрлі тәсілдері, сондай-ақ оқушылардың функционалдық сауаттылығын дамытуға бағытталған тапсырмалар ұсынылады. Сонымен қатар, құралда практикалық жаттығулар мен олимпиадалық деңгейдегі есептер де қарастырылған.
Бұл материал математика пәні мұғалімдеріне, оқушыларға және дайындық курстарының тыңдаушыларына пайдалы көмекші құрал бола алады.
Мазмұны
|
Кіріспе 1-БӨЛІМ. ЛОГАРИФМ ТҮСІНІГІ ЖӘНЕ НЕГІЗГІ ҚАСИЕТТЕРІ 1.1. Логарифм ұғымы және оның анықтамасы 1.2. Логарифмнің негізгі қасиеттері 1.3. Логарифмдік функция және оның графигі 2-БӨЛІМ. ЛОГАРИФМДЕРМЕН АМАЛДАР 2.1. Логарифмдердің қасиеттерін пайдаланып түрлендіру 2.2. Логарифмдердің қолданылуы (арифметикалық және геометриялық есептер) 2.3. Логарифмдік өрнектерді ықшамдау 3-БӨЛІМ. ЛОГАРИФМДІК ТЕҢДЕУЛЕР ЖӘНЕ ОЛАРДЫ ШЕШУ ӘДІСТЕРІ 3.1. Логарифмдік теңдеулердің түрлері 3.2. Логарифмдік теңдеулерді шешудің негізгі әдістері 3.3. Логарифмдік теңсіздіктер және оларды шешу жолдары 4-БӨЛІМ. ҚОЛДАНБАЛЫ ЕСЕПТЕР ЖӘНЕ ОЛИМПИАДАЛЫҚ ЕСЕПТЕР 4.1. Логарифмдерге қатысты өмірлік жағдайлардан алынған есептер 4.2. Логарифмдік теңдеулерге арналған күрделі есептер 4.3. Олимпиадалық және шығармашылық тапсырмалар Қорытынды Қосымшалар Пайдаланылған әдебиеттер |
4 5 6 8 10 11 13 15 17 19 21 24 25 28 29 31 |
Кіріспе
Логарифмдер және логарифмдік теңдеулер – орта мектеп математикасындағы маңызды тақырыптардың бірі. Ол оқушылардың алгебралық ойлау қабілетін дамытуға, функцияларды терең түсінуге және математикалық модельдеуді меңгеруге көмектеседі. Логарифмдік теңдеулерді шешу – оқушыларға қиындық тудыратын тақырыптардың бірі болғандықтан, оны тиімді оқыту әдістерін жетілдіру қажет.
Бұл әдістемелік құрал логарифмдер мен логарифмдік теңдеулерді оқытуда мұғалімдерге көмекші құрал ретінде әзірленді. Мұнда теориялық түсініктер, есептерді шешудің әдістері, логарифмдік өрнектерді ықшамдау және логарифмдік теңдеулерді шешудің түрлі тәсілдері қарастырылған. Сондай-ақ, құралда оқушылардың функционалдық сауаттылығын дамытуға бағытталған қолданбалы есептер мен олимпиадалық тапсырмалар қамтылған.
Өзекті мәселелер
1. Оқушылардың логарифмдік функцияларды және олардың қасиеттерін толық меңгермеуі.
2. Логарифмдік теңдеулерді шешуде қателіктер жіберуі.
3. Логарифмдік өрнектерді түрлендіру тәсілдерінің күрделілігі.
4. Оқушылардың математикалық ойлау дағдыларын дамыту қажеттілігі.
5. Логарифмдердің қолданбалы маңызын жеткілікті деңгейде түсінбеуі.
Осы мәселелерді шешу үшін әдістемелік құралда логарифмдік теңдеулерді шешудің тиімді тәсілдері ұсынылып, оқушылардың қызығушылығын арттыруға арналған шығармашылық және өмірмен байланысты тапсырмалар берілді.
Әдістемелік құралдың мақсаты
Оқушылардың логарифмдер мен логарифмдік теңдеулерді меңгеруін жеңілдету, есептерді шешу дағдыларын қалыптастыру және олардың математикалық сауаттылығын арттыру.
Міндеттері
• Логарифмдер туралы негізгі түсініктерді жүйелі түрде беру.
• Логарифмдік теңдеулерді шешудің тиімді әдістерін ұсыну.
• Оқушылардың логикалық ойлау қабілетін дамытуға арналған тапсырмалар енгізу.
• Логарифмдердің қолданбалы аспектілерін ашып көрсету.
• Олимпиадалық және шығармашылық деңгейдегі есептерді ұсыну арқылы оқушылардың математикалық қабілеттерін арттыру.
Күтілетін нәтижелер
• Оқушылар логарифм ұғымын және оның қасиеттерін терең меңгереді.
• Логарифмдік өрнектерді түрлендіру мен ықшамдауды еркін орындайды.
• Логарифмдік теңдеулерді әртүрлі әдістермен шешу дағдылары қалыптасады.
• Функционалдық сауаттылық артып, өмірлік есептерді шешу қабілеті дамиды.
• Олимпиадалық есептерге деген қызығушылық артады, оқушылар күрделі есептерді шешуге дағдыланады.
Бұл әдістемелік құрал математика пәні мұғалімдеріне, жоғары сынып оқушыларына және дайындық курстарының тыңдаушыларына арналған.
1-БӨЛІМ. ЛОГАРИФМ ТҮСІНІГІ ЖӘНЕ НЕГІЗГІ ҚАСИЕТТЕРІ
1.1. Логарифм ұғымы және оның анықтамасы
1. Логарифм дегеніміз не?
Логарифм – бұл белгілі бір негіздегі дәрежені анықтайтын математикалық амал. Егер:
![]()
теңдігі орындалса, онда b санының a негізі бойынша логарифмі x-ке тең болады және ол былай жазылады:
![]()
Мұндағы:
• a – логарифм негізі (a > 0, a \neq 1);
• b – логарифм алынатын сан (b > 0);
• x – логарифм мәні, яғни дәрежелік көрсеткіш.
Мысалдар:
![]()
![]()
![]()
2. Логарифмнің түрлері
1. Ондық логарифм – негізі 10 болатын логарифм. Ол көбінесе ғылыми есептеулерде қолданылады.
![]()
Кейде ондық логарифмді жазғанда негіз көрсетілмейді:
![]()
2. Натурал логарифм – негізі e (шамамен 2.718) болатын логарифм. Ол ln деп белгіленеді:
![]()
Натурал логарифм экспоненциалдық және логарифмдік функцияларды зерттеуде қолданылады.
3. Екілік логарифм – негізі 2 болатын логарифм. Ол компьютерлік ғылымдарда және ақпарат теориясында жиі кездеседі:
![]()
3. Логарифмнің қолданылуы
Логарифм көптеген ғылым салаларында қолданылады:
• Физика – дыбыс деңгейін (децибелмен) және жер сілкінісінің күшін (Рихтер шкаласы) өлшеуде.
• Экономика – пайыздық өсімді есептеуде.
• Компьютерлік ғылымдар – алгоритмдердің уақыт күрделілігін талдауда.
• Химия – рН деңгейін анықтауда.
1.2. Логарифмнің негізгі қасиеттері
Логарифмдердің негізгі қасиеттері олардың арифметикалық есептеулерде және түрлендірулерде қолданылуын жеңілдетеді.
1. Көбейтіндінің логарифмі
Кез
келген a
> 0, a![]() 1 және b
> 0, c
> 0 үшін:
1 және b
> 0, c
> 0 үшін:
![]()
Дәлелдеме:
Егер ![]() әне
әне ![]() ,
онда
,
онда
![]()
Көбейтсек:
![]()
Дәрежелерді қосу ережесі бойынша:
![]()
Демек, логарифм анықтамасы бойынша:
![]()
Мысал:
![]()
2. Бөліндінің логарифмі
Кез келген a > 0, а ≠1 және b > 0, c > 0 үшін:
![]()
Дәлелдеме:
Егер ![]() және
және ![]() ,
онда
,
онда
![]() .
.
Бөлсек:
![]()
Дәрежелерді азайту ережесі бойынша:
![]()
Демек,
![]()
Мысал:
![]()
3. Дәреженің логарифмі
Кез келген a > 0, a ≠1 және b > 0, n – кез келген нақты сан үшін:
![]()
Дәлелдеме:
Егер ![]() ,
онда
,
онда
![]() .
.
Дәрежеге көтерсек:
![]()
Дәрежелерді көбейту ережесі бойынша:
![]()
Демек,
![]() .
.
Мысал:
![]()
4. Негізді өзгерту формуласы
Кез келген a > 0, a ≠1 және b > 0, c > 0, c \neq 1 үшін:

Бұл формула логарифмдерді әртүрлі негізге ауыстыру үшін қолданылады.
Мысал:

Егер есептеуде ондық логарифм қолдансақ:
![]()
5. Негізі мен саны бірдей болған жағдайда
Кез келген a > 0,
a ![]() 1
үшін:
1
үшін:
![]() .
.
Мысал:
![]() .
.
6. Бірліктің логарифмі
Кез
келген a
> 0, a
![]() 1 үшін:
1 үшін:
![]()
Мысал:
![]()
Логарифмнің бұл қасиеттері оны жеңілдетуге және түрлендіруге көмектеседі. Оларды білсеңіз, кез келген логарифмдік есептеулерді оңай шығара аласыз.
1.3. Логарифмдік функция және оның графигі
1. Логарифмдік функцияның анықтамасы
Логарифмдік функция — бұл келесі түрде берілген функция:
![]()
Мұндағы:
• a > 0,
a ![]() 1 –
логарифмнің негізі;
1 –
логарифмнің негізі;
• x > 0 – тәуелсіз айнымалы (логарифм тек оң сандар үшін анықталған).
Логарифмдік функция көрсеткіштік функцияның кері функциясы болып табылады. Егер:
![]()
болса, онда оған сәйкес көрсеткіштік функция:
![]()
2. Логарифмдік функцияның қасиеттері
1. Анықталу облысы: x > 0 (тек оң сандар үшін анықталған).
2.
Мәндер жиыны: ![]() (барлық нақты сандар).
(барлық нақты сандар).
3.
Түбір нүктесі: x
= 1, себебі ![]()
4. Монотондылық:
• Егер a > 1, онда функция өседі.
• Егер 0 < a < 1, онда функция кемиді.
5. Тіктік асимптота: x = 0 (логарифмдік функцияның графигі y-осіне жақындайды, бірақ оны ешқашан қимайды).
3. Логарифмдік функцияның графигі
Графикті тұрғызу үшін бірнеше маңызды нүктелерді есептейік:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Енді осы графиктерді тұрғызайық.
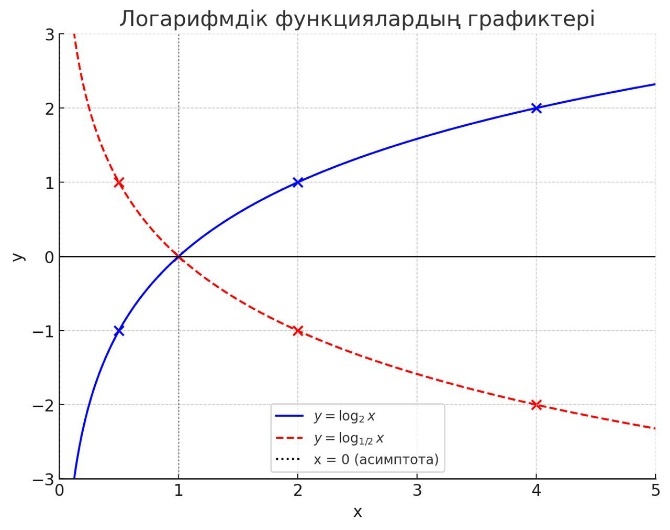
Графикте екі түрлі логарифмдік функция көрсетілген:
Көк
сызық: ![]() (өсетін функция, себебі a >
1).
(өсетін функция, себебі a >
1).
Қызыл пунктирлі сызық:
![]() (кемитін функция, себебі 0 < a <
1).
(кемитін функция, себебі 0 < a <
1).
Көріп тұрғанымыздай, логарифмдік функцияның графигі оң жақ жартыжазықтықта орналасады және x = 0 тіктік асимптотасына жақындайды, бірақ оны қимайды.
2-БӨЛІМ. ЛОГАРИФМДЕРМЕН АМАЛДАР
2.1. Логарифмдердің қасиеттерін пайдаланып түрлендіру
Логарифмдік өрнектерді түрлендіру үшін олардың негізгі қасиеттерін пайдалану керек.
1. Көбейтіндінің логарифмі
![]()
Мысал:
![]()
2. Бөліндінің логарифмі
![]()
Мысал:
![]()
3. Дәреженің логарифмі
![]()
Мысал:
![]()
4. Негізді өзгерту формуласы

Мысал:

5. Күрделі өрнектерді түрлендіру мысалдары
Мысал 1
Өрнекті ықшамдаңыз:
![]()
Шешуі:
![]()
![]()
![]()
Енді мәндерді қоямыз:
2 + 3 - 4 = 1.
Жауабы: 1.
Мысал 2
![]()
Шешуі:
![]()
![]()
Енді өрнекті ықшамдаймыз:
![]()
Жауабы: 3.
Логарифмдік өрнектерді түрлендіру үшін логарифмнің негізгі қасиеттерін білу өте маңызды. Түрлендірулерді дұрыс орындау логарифмдік теңдеулерді шешуде де үлкен көмегін тигізеді.
2.2. Логарифмдердің қолданылуы (арифметикалық және геометриялық есептер)
Логарифмдер тек теориялық ұғым ғана емес, оларды күнделікті өмірде, физикада, экономикада, статистикада, геометрияда, ақпараттық технологияларда және басқа да салаларда қолдануға болады.
1. Арифметикалық есептер
Мысал 1: Үлкен сандарды жеңіл есептеу
Кейде үлкен сандарды көбейту, бөлу, дәрежеге шығару немесе түбір табу қиынға соғады. Бұл жағдайда логарифмдер есептеуді оңайлатады.
Мысал:
Есептеңіз:
![]()
Егер тікелей есептесек, көбейту қиын болуы мүмкін. Бірақ логарифмді қолдансақ:
![]()
![]()
Көбейтуді логарифм арқылы түрлендірсек:
![]()
Демек,
![]()
Жауабы: 2 097 152.
Мысал 2: Банк депозиті (пайыздық өсім)
Банкке жылдық 10% өсіммен 500 000 теңге салынды. Қанша жылдан кейін ақша 1 000 000 теңгеге жетеді?
Формула:
![]()
Мұндағы:
• A – соңғы сома (1 000 000).
• P – бастапқы сома (500 000).
• r – пайыздық мөлшерлеме (10% = 0.1).
• t – жыл саны.
Өрнекті теңдеуге айналдырайық:
![]()
Екі жақты 500 000-ға бөлеміз:
![]()
Логарифм аламыз:
![]()
Негізді өзгерту формуласын қолданамыз:

Енді нақты мәнін есептейік.
Жауабы: Шамамен 7.27 жыл немесе 7 жыл 3 ай ішінде ақша 1 000 000 теңгеге жетеді.
2. Геометриялық есептер
Мысал 3: Үлкен мәндерді логарифм арқылы жеңілдету
Үшбұрыштың ауданы келесі формуламен берілсін:
![]()
Мұндағы p – жартылай периметр:
![]()
Берілген:
• a = 15, b = 26, c = 37.
Үшбұрыштың ауданын есептеу керек.
Шешуі:
Алдымен жартылай периметрді табайық:
![]()
Аудан формуласына қоямыз:
![]()
Бұл үлкен сандармен жұмыс істеуді қиындатады. Оны логарифмдік түрлендіру арқылы оңайлатуға болады:
![]()
Жауабы: Үшбұрыштың ауданы 156 бірлік².
2.3. Логарифмдік өрнектерді ықшамдау
Логарифмдік өрнектерді ықшамдау үшін логарифмдердің негізгі қасиеттерін қолданамыз.
1. Логарифмдердің негізгі қасиеттері:
1. Көбейтіндінің логарифмі:
![]()
2. Бөліндінің логарифмі:
![]()
3. Дәреженің логарифмі:
![]()
4. Негізді өзгерту формуласы:

2. Өрнектерді ықшамдау мысалдары
Мысал 1
Өрнекті ықшамдаңыз:
![]()
Шешуі:
![]()
![]()
![]()
Енді өрнекті ықшамдаймыз:
3 + 2 - 1 = 4.
Жауабы: 4.
Мысал 2
Өрнекті ықшамдаңыз:
![]()
Шешуі:
![]()
![]()
![]()
Енді есептейміз:
3 + 2 - 4 = 1.
Жауабы: 1.
Мысал 3
Өрнекті ықшамдаңыз:
![]()
Шешуі:
![]()
![]()
![]()
Енді есептейміз:
3 - 2 + 2 = 3.
Жауабы: 3.
3. Қиынырақ есептер
Мысал 4
Өрнекті ықшамдаңыз:
![]()
Шешуі:
![]()
![]() .
.
Жауабы: 3.
Мысал 5
Өрнекті ықшамдаңыз:
![]()
Шешуі:
Алдымен
![]() түрлендірейік:
түрлендірейік:
![]() .
.
![]()
Жауабы:
![]()
Логарифмдік өрнектерді ықшамдау үшін негізгі қасиеттерді қолдану керек.
• Көбейту → қосуға айналады.
• Бөлу → азайтуға айналады.
• Дәреже → көбейткішке айналады.
• Қарапайым мәндерді пайдаланып, логарифмдерді оңайлату қажет.
3-БӨЛІМ. ЛОГАРИФМДІК ТЕҢДЕУЛЕР ЖӘНЕ ОЛАРДЫ ШЕШУ ӘДІСТЕРІ
3.1. Логарифмдік теңдеулердің түрлері
Логарифмдік теңдеулер — белгісіз айнымалы логарифм белгісінің ішінде тұрған теңдеулер. Мұндай теңдеулерді шешу үшін логарифмдердің қасиеттерін және теңдеулерді шешу әдістерін білу қажет.
Логарифмдік теңдеулердің негізгі төрт түрі бар:
1. Негіздері бірдей логарифмдік теңдеулер
Бұл теңдеулердің жалпы түрі:
![]()
Мұнда негіздер бірдей болғандықтан, логарифмдердің ішіндегі өрнектер тең болады:
![]()
Мысал:
![]()
Шешімі:
![]()
![]()
![]()
![]()
Жауабы:
![]()
2. Логарифмдік теңдеулерді дәрежелік түрге келтіру
Кейбір теңдеулерді экспоненциалдық (дәрежелік) түрге келтіруге болады. Жалпы түрі:
![]()
Бұл теңдеуді дәрежеге шығару әдісімен шешеміз:
![]()
Мысал:
![]()
Шешімі:
![]()
Жауабы:![]()
3. Логарифмдік теңдеулерді түрлендіру арқылы шешу
Кейбір теңдеулерде бірнеше логарифм болады, оларды логарифмдік қасиеттерді пайдаланып ықшамдауға болады.
Мысал:
![]()
Шешімі:
Логарифмдердің қосындысын көбейтінді түрінде жазамыз:
![]()
Енді дәрежелік түрге келтіреміз:
![]()
![]()
![]()
Квадраттық теңдеуді шешеміз:
![]()
![]()
Бірақ логарифмнің анықталу облысын тексереміз:
![]()
![]()
![]() анықталу облысына
кірмейді!
анықталу облысына
кірмейді!
Жауабы:
![]()
4. Күрделі логарифмдік теңдеулер
Күрделі логарифмдік теңдеулерде логарифмдерді айнымалы енгізу арқылы шешеміз.
Мысал:
![]()
Шешімі:
Қосындыны көбейтінді түріне келтіреміз:
![]()
Енді дәрежеге шығарамыз:
![]()
![]()
![]()
Квадраттық теңдеуді шешеміз:
![]()
![]()
Анықталу облысын тексереміз:
![]()
![]() жарамсыз!
жарамсыз!
Жауабы:
![]()
Логарифмдік теңдеулердің төрт негізгі түрі бар:
1. Негіздері бірдей теңдеулер → ішіндегі өрнектерді теңестіру.
2. Дәрежеге шығару әдісі → экспоненциалдық түрге ауыстыру.
3. Қасиеттерді пайдалану → логарифмдерді ықшамдау.
4. Айнымалы енгізу әдісі → күрделі теңдеулерді оңайлату.
3.2. Логарифмдік теңдеулерді шешудің негізгі әдістері
Логарифмдік теңдеулерді шешудің бірнеше негізгі әдістері бар. Олардың әрқайсысы белгілі бір түрдегі теңдеулерді шешуге қолданылады.
1-әдіс: Негіздері бірдей логарифмдердің аргументтерін теңестіру
Егер теңдеудің екі жағында бірдей негізді логарифмдер болса, онда олардың аргументтерін теңестіруге болады.
Мысал 1:
![]()
![]()
![]()
![]()
![]()
![]()
Жауабы:
![]()
2-әдіс: Логарифмнің анықталу облысын ескере отырып, дәрежеге шығару
Егер теңдеудің бір жағында логарифм, ал екінші жағында сан болса, онда оны дәрежеге шығару арқылы шешуге болады.
Мысал 2:
![]()
![]()
![]()
![]()
![]()
3-әдіс: Логарифмдік теңдеулерді түрлендіру
Егер теңдеуде бірнеше логарифм болса, онда оларды біріктіру арқылы ықшамдап, шешім табуға болады.
Мысал 3:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4-әдіс: Айнымалы енгізу әдісі
Күрделі логарифмдік теңдеулерде жаңа айнымалы енгізіп, оны квадраттық немесе сызықтық теңдеуге айналдыруға болады.
Мысал 4:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
5-әдіс: Негізді өзгерту және жаңа айнымалы енгізу
Кейбір теңдеулерді шешу үшін негізді өзгертіп, жаңа айнымалы енгізу тиімді.
Мысал 5:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Логарифмдік теңдеулерді шешудің негізгі бес әдісі бар:
1. Негіздері бірдей логарифмдерді теңестіру.
2. Дәреже түріне айналдыру.
3. Қасиеттерді қолданып түрлендіру.
4. Айнымалы енгізу.
5. Негізді өзгерту және жаңа айнымалы қолдану.
3.3. Логарифмдік теңсіздіктер және оларды шешу жолдары
Логарифмдік теңсіздіктер – белгісіз айнымалы логарифм белгісінің ішінде тұрған теңсіздіктер. Мұндай теңсіздіктерді шешу үшін логарифмдік функцияның қасиеттерін, теңсіздіктердің шешу әдістерін және анықталу облысын білу қажет.
1. Логарифмдік теңсіздіктерді шешу әдістері
Логарифмдік теңсіздіктерді шешудің негізгі үш әдісі бар:
1. Негіздері бірдей логарифмдік теңсіздіктерді шешу.
2. Логарифмдік теңсіздіктерді дәрежелік түрде жазу.
3. Жаңа айнымалы енгізу арқылы шешу.
1-әдіс: Негіздері бірдей логарифмдерді салыстыру
Егер теңсіздіктің екі жағында бірдей негізді логарифмдер болса, онда олардың ішіндегі өрнектерін салыстыруға болады.
Мысал 1:
![]()
![]()
![]()
![]()
![]()
![]()
Анықталу облысын тексеру:
![]()
![]()
![]()
![]()
2-әдіс: Логарифмдік теңсіздіктерді дәрежелік түрде жазу
Егер теңсіздіктің бір жағында логарифм, ал екінші жағында сан болса, онда оны дәрежеге шығару арқылы шешуге болады.
Мысал 2:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3-әдіс: Жаңа айнымалы енгізу
Кейбір теңсіздіктерде логарифмдерді айнымалы ретінде алып, теңсіздікті жеңілдетуге болады.
Мысал 3:
![]()
![]()
![]()
![]()
![]()
![]()
Квадраттық теңсіздікті шешеміз:
Квадраттық теңдеудің түбірлерін табамыз:

![]()
![]()
![]()

Логарифмдік теңсіздіктерді шешудің негізгі ережелері
1. Негізі 1-ден үлкен логарифмдік функция өспелі, сондықтан:
• Егер a > 1 болса, онда:
![]()
• Егер 0 < a < 1 болса, онда:
![]()
(Белгі өзгертіледі!)
2. Логарифмнің анықталу облысын тексеру қажет:
• Логарифмнің ішіндегі өрнек әрқашан нөлден үлкен болуы керек.
Логарифмдік теңсіздіктерді шешудің үш негізгі әдісі бар:
1. Негіздері бірдей логарифмдерді салыстыру.
2. Логарифмдерді дәрежеге шығару.
3. Жаңа айнымалы енгізу арқылы теңсіздікті жеңілдету.
4-БӨЛІМ. ҚОЛДАНБАЛЫ ЕСЕПТЕР ЖӘНЕ ОЛИМПИАДАЛЫҚ ЕСЕПТЕР
4.1. Логарифмдерге қатысты өмірлік жағдайлардан алынған есептер
Логарифмдер математикада ғана емес, күнделікті өмірде де кеңінен қолданылады. Олардың көмегімен жер сілкінісінің күші, радиоактивті ыдырау, халық санының өсуі, дыбыс деңгейі және басқа да көптеген процестер сипатталады.
1-есеп. Жер сілкінісінің Рихтер шкаласы
Жер сілкінісінің магнитудасын анықтау үшін Рихтер шкаласы қолданылады:
![]()
мұндағы:
![]()
![]()
![]()
Мәселе:
Егер бір жер сілкінісінің магнитудасы 6,5, ал екіншісі 5,2 болса, бірінші жер сілкінісі екіншісіне қарағанда қанша есе күшті?
Шешімі:
Берілген формуладан екі магнитуда үшін қарқындылықтардың қатынасын табамыз:
![]()
![]()
![]()
Жауабы: Бірінші жер сілкінісі екіншісіне қарағанда 20 есе күшті.
2-есеп. Радиоактивті ыдырау
Радиоактивті заттың ыдырау жылдамдығы жартылай ыдырау уақыты арқылы есептеледі:
![]()
мұндағы:
![]()
![]()
![]()
![]()
Мәселе:
Радиоактивті изотоптың жартылай ыдырау уақыты 24 жыл. Егер бастапқыда 100 грамм радиоактивті зат болса, 72 жылдан кейін қанша грамм қалады?
Шешімі:
![]()
![]()
![]()
Жауабы: 72 жылдан кейін 12,5 грамм радиоактивті зат қалады.
3-есеп. Ақша жинақтау (пайыздық өсім)
Банкте жылдық 8% мөлшерлемемен салым ашылды. Егер бастапқыда 100 000 теңге салынса, 10 жылдан кейін қанша ақша жиналады? (Проценттер капиталдандырылады, яғни әр жыл сайын өсім қосылып отырады).
Формула:
![]()
мұндағы:
![]()
![]()
![]()
![]()
Шешімі:
![]()
![]()
![]()
Жауабы: 10 жылдан кейін 215 890 теңге жиналады.
4-есеп. Дыбыс деңгейін есептеу (децибел шкаласы)
Дыбыс деңгейі децибелмен (dB) өлшенеді және келесі формуламен анықталады:
![]()
мұндағы:
![]()
![]()
![]()
Мәселе:
Егер қаланың шу деңгейі 80 дБ, ал ауылдың шу деңгейі 40 дБ болса, қаладағы шу ауылмен салыстырғанда қанша есе күшті?
Шешімі:


![]()
Жауабы: Қаладағы шу ауылға қарағанда 10 000 есе күшті.
Бұл бөлімде логарифмдердің өмірлік жағдайларда қолданылуын қарастырдық. Логарифмдер:
✔ Жер сілкінісін өлшеуде,
✔ Радиоактивті ыдырауды есептеуде,
✔ Банк салымдарын болжауда,
✔ Дыбыс деңгейін анықтауда қолданылады.
4.2. Логарифмдік теңдеулерге арналған күрделі есептер
Бұл бөлімде логарифмдік теңдеулерді шешудің әртүрлі әдістерін қолдануды талап ететін күрделі есептер қарастырылады. Мұндай теңдеулер көбінесе логарифмдік қасиеттерді, жаңа айнымалы енгізу әдісін, логарифмдеу тәсілін және теңдеулер жүйесін қолдануды қажет етеді.
1-есеп. Логарифмдерді бір негізге келтіру әдісі
Теңдеуді шешіңіз:
![]()
Шешімі:
1. Логарифмдердің негізін
бірдей ету үшін ![]() түрлендіруін
қолданамыз:
түрлендіруін
қолданамыз:
![]()
2. Жаңа айнымалы енгіземіз:
![]()
Сонда теңдеу:
![]()
3. Ортақ көбейткішке келтіреміз:
![]()
4. t-ны табамыз:
t = 2
5. t-ның орнына қайта қоямыз:
![]()
6. Логарифмнің анықтамасы бойынша:
![]()
![]()
![]()
7. Анықталу облысы бойынша x - 3 > 0 \Rightarrow x > 3, яғни түбір жарамды.
Жауабы: x = 7.
2-есеп. Жаңа айнымалы енгізу әдісі
Теңдеуді шешіңіз:
![]()
Шешімі:
1. Логарифмдердің қасиетін қолданамыз:
![]()
2. Логарифмнің анықтамасы бойынша:
![]()
![]()
![]()
3. Квадрат теңдеуді шешеміз:

4. Анықталу облысын тексереміз:
![]()
![]()
![]()
![]()
![]()
Бұл бөлімде логарифмдік теңдеулерді шешудің күрделі тәсілдері қарастырылды:
Логарифмдерді бір негізге келтіру
Жаңа айнымалы енгізу
Квадрат теңдеулерге келтіру
Логарифмдік теңдеулер жүйесін шешу
Теңсіздіктерді шешу әдістері
Бұл тәсілдер логарифмдік теңдеулерді терең түсінуге және математикалық дағдыларды дамытуға көмектеседі.
4.3. Олимпиадалық және шығармашылық тапсырмалар
Бұл бөлімде логарифмдерге қатысты олимпиадалық есептер, шығармашылық тапсырмалар және логикалық ойлауды талап ететін есептер беріледі. Мұндай тапсырмалар оқушылардың математикалық интуициясын, логарифмдік қасиеттерді қолдану дағдыларын, және күрделі есептерді талдау қабілетін дамытады.
1-есеп. Логарифмдік өрнектің мәнін табу
Берілген өрнектің мәнін табыңыз:
![]()
Шешімі:
Логарифмдердің қасиеттерін қолданып, әрбір көбейткішті түрлендірейік:

![]()

Жауабы:![]()
2-есеп. Логарифмдік теңдеуді ерекше тәсілмен шешу
Берілген теңдеуді шешіңіз:
![]()
Шешімі:
1. Логарифмдерді бір негізге келтіреміз:

2. Жаңа айнымалы енгіземіз:
![]()
Осыны теңдеуге қоямыз:


![]()
3. Квадраттық теңдеу аламыз:
![]()
Дискриминантты есептейміз:
![]()

4. Айнымалыны кері ауыстырамыз:
![]()
Жауабы:
![]()
3-есеп. Логарифмдік сиқырлы квадрат
Төмендегі логарифмдік теңдеулерден сандық өрнек құрып, бос орынды толтырыңыз:
|
|
|
? |
|
|
? |
|
|
? |
|
|
Шешімі:
• Қатарлар мен бағандардағы мәндерді зерттейік:
![]()
![]()
• Жетіспейтін мәндерді анықтаймыз:
• Ортаңғы
элемент:![]()
• Жоғарғы оң жақ
бұрыш: ![]()
• Төменгі сол жақ
бұрыш: ![]()
![]()
![]()
![]()
Жауабы:
Ортаңғы
элемент ![]()
Бұл бөлімдегі тапсырмалар логарифмдік өрнектерді ықшамдауға, күрделі теңдеулерді шешуге, және шығармашылықпен ойлауға бағытталған. Мұндай есептер олимпиадаларда, жоғары деңгейлі емтихандарда, және мектеп оқушыларының логикалық ойлау қабілетін дамытуда өте пайдалы.
Қорытынды
Бұл әдістемелік құрал логарифмдер тақырыбын толық қамтып, оқушылардың теориялық білімін бекітуге, есеп шығару дағдыларын дамытуға және олимпиадалық күрделі есептерді шешуге бағытталған.
Қолжеткізілген нәтижелер:
Логарифмнің негізгі түсініктерін меңгеру – оқушылар логарифмнің анықтамасын, қасиеттерін және графигін толық түсінеді.
Логарифмдік өрнектермен жұмыс жасау дағдысы қалыптасты – логарифмдік өрнектерді түрлендіру, ықшамдау және қолдану әдістерін меңгерді.
Логарифмдік теңдеулер мен теңсіздіктерді шешудің тиімді тәсілдерін игеру – оқушылар әртүрлі типтегі логарифмдік теңдеулерді шешуді үйренді.
Логарифмдердің қолданбалы маңызын түсіну – нақты өмірлік жағдайлардан алынған есептер арқылы логарифмдердің күнделікті өмірдегі рөлін ұғынды.
Олимпиадалық есептерді шешу қабілеті жетілді – жоғары деңгейдегі логикалық тапсырмаларды орындау арқылы оқушылардың математикалық ойлау қабілеті дамыды.
Практикалық маңыздылығы:
Бұл құрал мұғалімдерге оқыту процесін жеңілдетуге, оқушыларға өздігінен дайындалуға, ал олимпиадаға қатысушыларға математикалық логикасын дамытуға көмектесті. Әдістемелік материалдар оқушылардың логарифмдер тақырыбын терең меңгеруіне, қолданбалы есептерді шешуге және функционалдық сауаттылығын арттыруға ықпал етті.
Жалпы, бұл әдістемелік құрал логарифмдер тақырыбын жан-жақты меңгеруге арналған тиімді материал болып табылады. Ол мұғалімдерге, оқушыларға, пәндік олимпиадаға қатысушыларға және математикаға қызығатын кез келген адамға пайдалы көмекші ресурс бола алады.
Қосымшалар
1. Логарифмдік функциялардың қасиеттері мен графиктері
Логарифмдік функцияның жалпы түрі:
![]()
мұндағы
![]()
Логарифмдік функцияның негізгі қасиеттері:
Анықталу облысы: x > 0.
Мәндер
жиыны: ![]()
Түйін нүкте: x = 1,
себебі![]()
Өсуі немесе кемуі:
• Егер a > 1, онда функция өсетін (монотонды).
• Егер 0 < a < 1, онда функция кемитін (монотонды).
Жартылай
симметриялы: ![]() функциясының графигі (0;1)
нүктесі арқылы өтеді.
функциясының графигі (0;1)
нүктесі арқылы өтеді.
Графиктері:
• a > 1 үшін логарифмдік функция өседі.
• 0 < a < 1 үшін логарифмдік функция кемиді.
• ![]() графигі әрқашан Оу осін қиып
өтпейді, тек оған асимптоталық жақындайды.
графигі әрқашан Оу осін қиып
өтпейді, тек оған асимптоталық жақындайды.
2. Логарифмдік теңдеулерді шешудің алгоритмдері
Алгоритм 1: Логарифмдерді бір негізге келтіру
Қадамдар:
1. Барлық логарифмдерді бірдей негізге келтіру.
2. Логарифмдік өрнектерді ықшамдау.
3. Логарифмдік теңдеулердің анықталу облысын (ОДЗ) анықтау.
4. Логарифмдік теңдеуді шешу (екі жақты логарифмдеу немесе жаңа айнымалы енгізу).
5. Табылған түбірлерді ОДЗ-ға сәйкес тексеру.
Мысал:
Шешіңіз:
![]()
Шешімі:
1. Логарифмдердің негізі бірдей болғандықтан, аргументтер тең:
x + 1 = 5
2. x = 4.
3. x > -1 шартын ескеріп, x = 4 жарамды деп аламыз.
Жауабы: x = 4.
Алгоритм 2: Жаңа айнымалы енгізу
Қадамдар:
1. Логарифмдік өрнекті жаңа айнымалымен белгілеу, мысалы:
![]()
2. Теңдеуді t-ге қатысты шешу.
3. Шыққан шешімді бастапқы айнымалыға кері қою арқылы x-тің мәнін табу.
4. Нәтижелерді тексеру.
Мысал:
Шешіңіз:
![]()
Шешімі:
1.Логарифмдердің қасиетін пайдаланып, көбейтінді түрінде жазамыз:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5. Анықталу облысы бойынша x > 8, сондықтан x = 9.
Жауабы: x = 9.
3. Өзіндік жұмысқа арналған тапсырмалар
Тапсырма 1: Логарифмдік өрнектерді ықшамдау
![]()
![]()
![]()
![]()
Тапсырма 2: Логарифмдік теңдеулерді шешу
![]()
![]()
![]()
![]()
Тапсырма 3: Логарифмдік теңсіздіктерді шешу
![]()
![]()
![]()
![]()
Пайдаланылған әдебиеттер
1. Алгебра және анализ бастамалары, 11-сынып, ҚР Білім және ғылым министрлігі ұсынған оқулық.
2. Логарифмдер және олардың қасиеттері, Бекбоев С., Алматы: Мектеп баспасы, 2015.
3. Қолданбалы математика: логарифмдік теңдеулер мен теңсіздіктер, Қайырбаев Е., Астана, 2018.
4. Математикалық талдау негіздері, Фихтенгольц Г.М. – М.: Наука, 2002.
5. Higher Algebra, Hall & Knight, Cambridge University Press, 2010.
6. Logarithmic and Exponential Functions, Stewart J., Cengage Learning, 2016.
7. ҚР ҰБТ және пәндік олимпиадаларға арналған әдістемелік құралдар – www.testcenter.kz.
8. Орта білім беру стандарттары мен оқу бағдарламалары, ҚР БҒМ – www.nao.kz.
9. Wolfram Alpha – www.wolframalpha.com (логарифмдік функциялардың графигін салу және есептерді тексеру үшін).
10. Алгебра: 10-11 сыныптарға арналған есептер жинағы, С. Жұмағұлов, Алматы: Мектеп, 2019.
11. Математика: мектеп және олимпиада есептері, Әлімқұлов А., Астана: Фолиант, 2020.
12. Жоғары математиканың негіздері, Курош А.Г., М.: Наука, 1980.
13. Математикалық логика және оның қолданылуы, Клебанов Л., Алматы: Рауан, 1995.
14. Логарифмдік теңдеулерді шешу әдістері, Дүйсенов Қ., Алматы: Арман-ПВ, 2017.
15. Қазіргі заманғы математикалық әдістер, Брусиловский А., Мәскеу: Мир, 2001.
33















